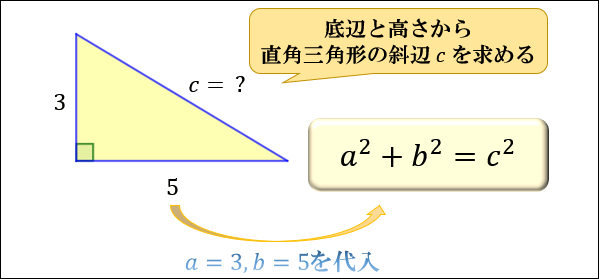
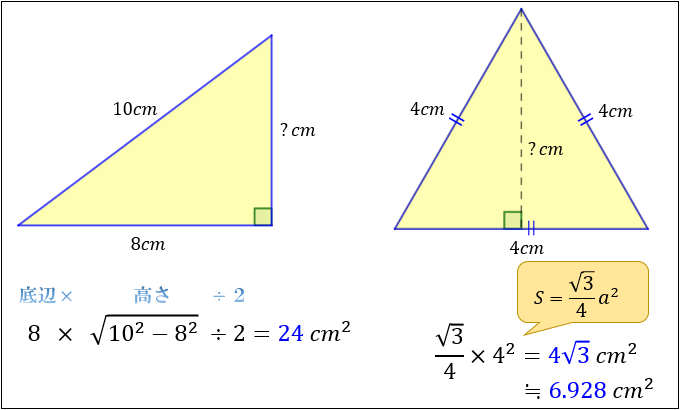
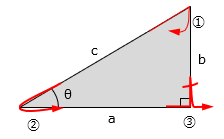
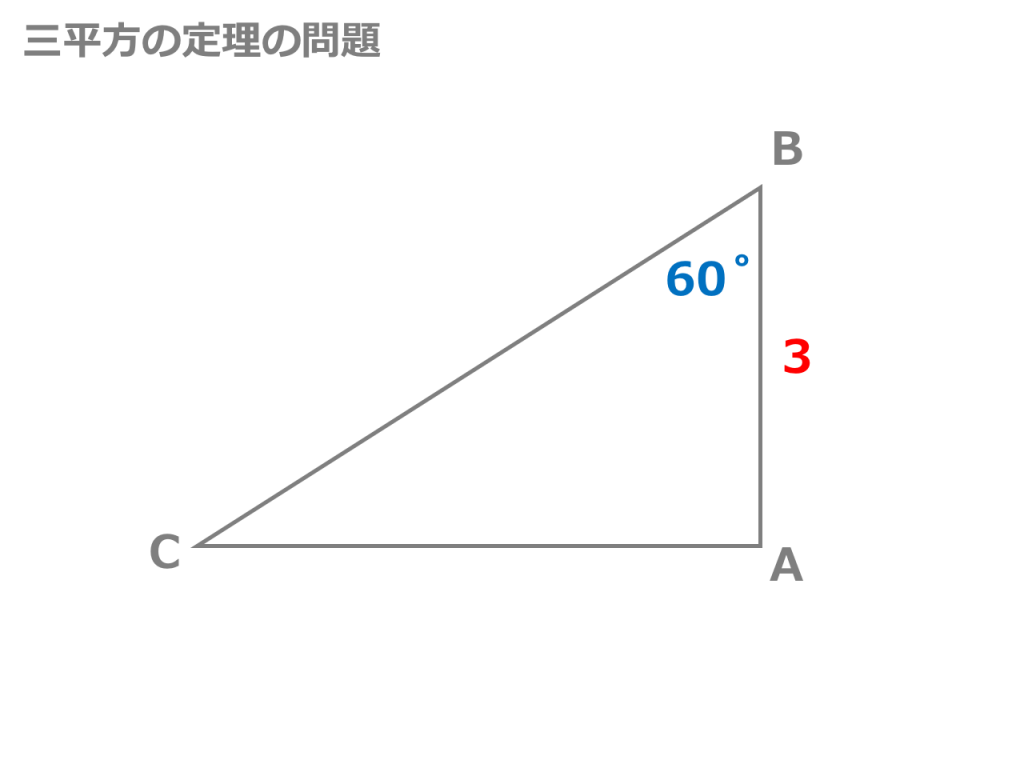
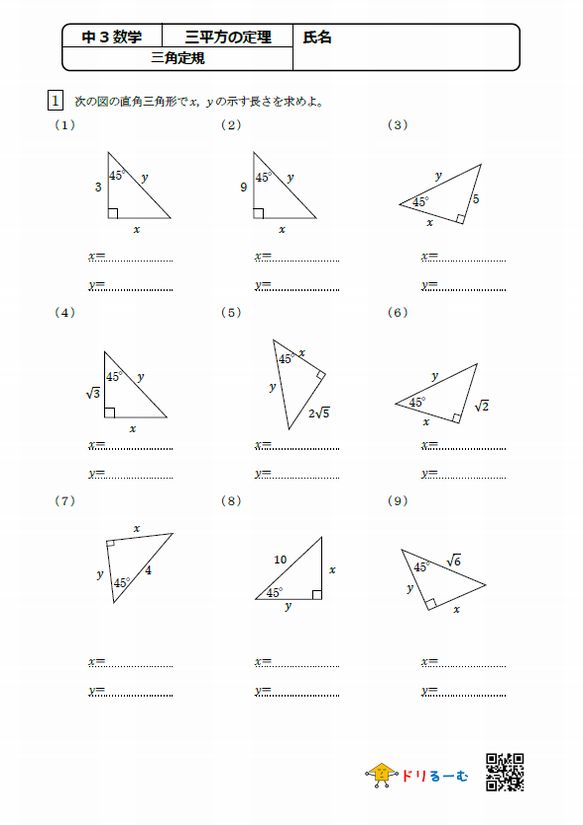
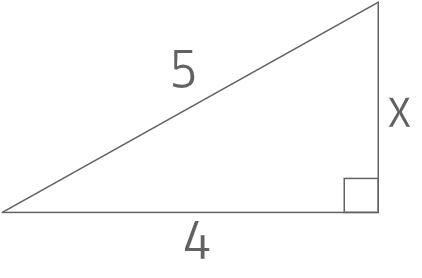
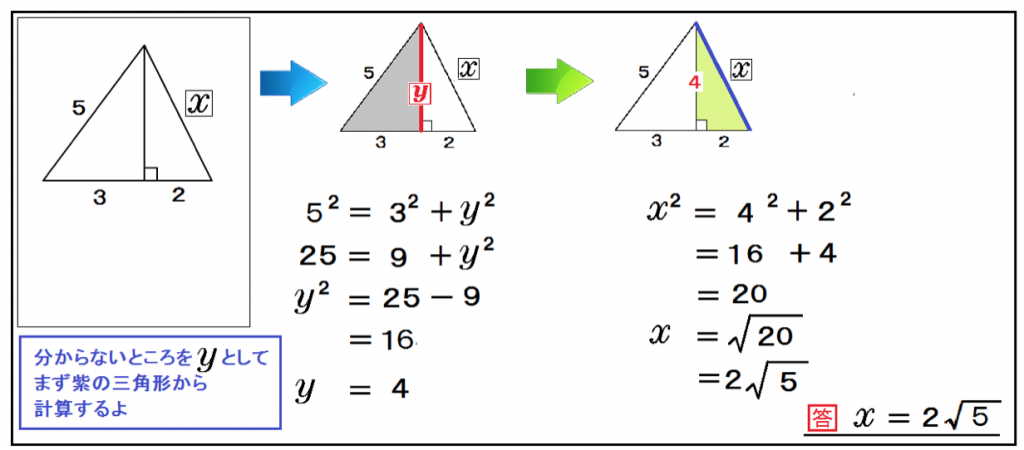
三平方の定理 発展問題まとめ お疲れ様でした! 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが
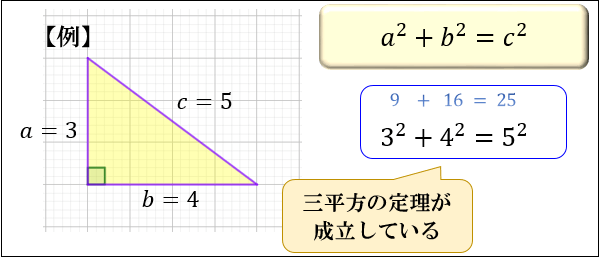
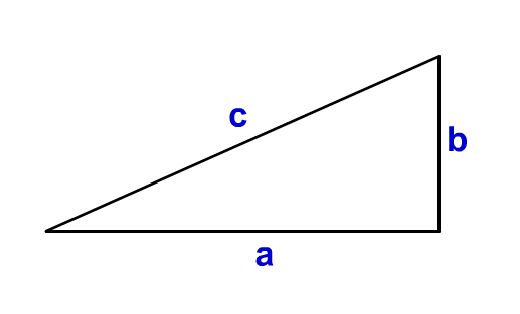
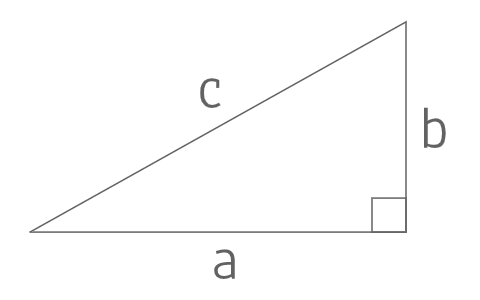
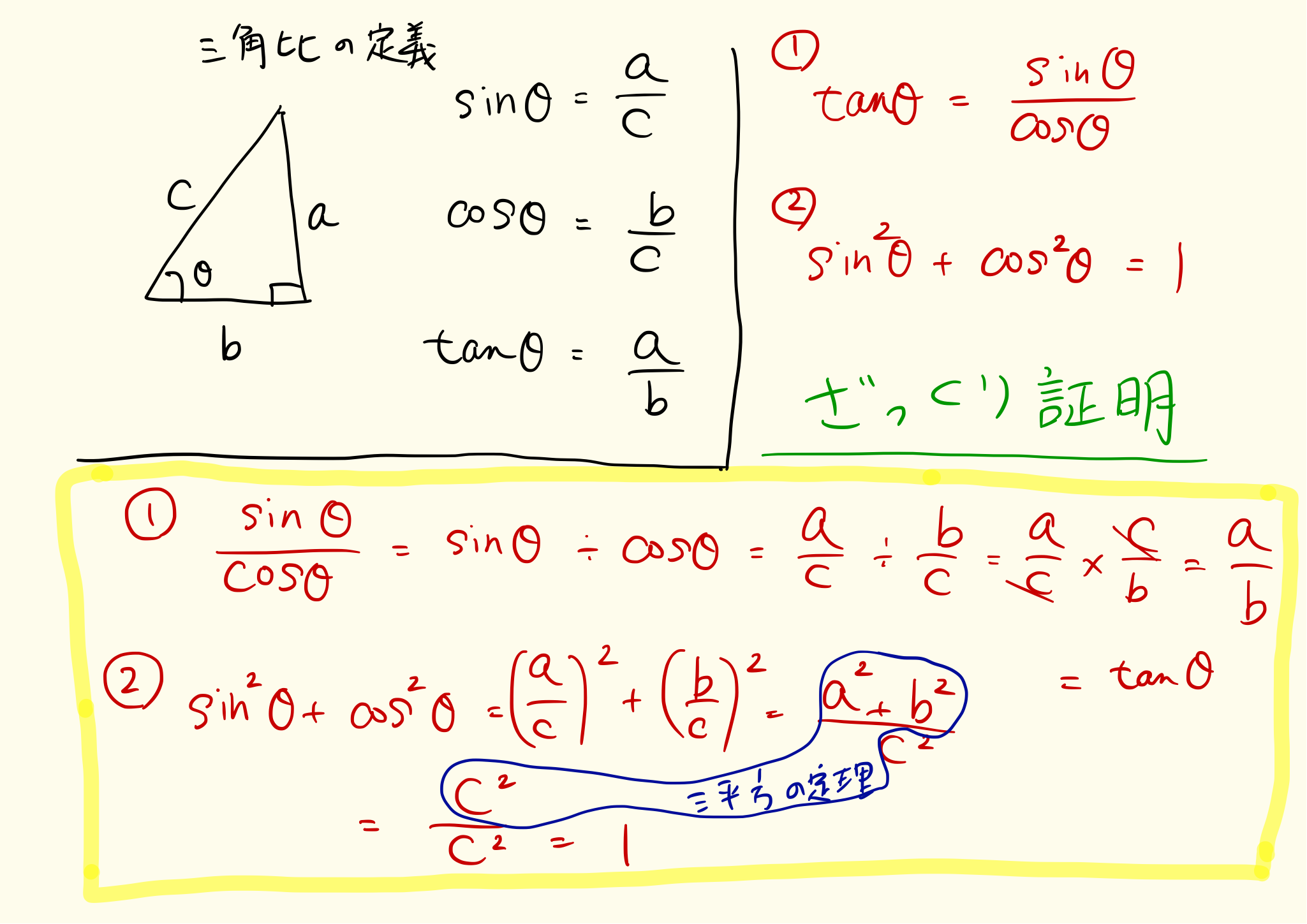
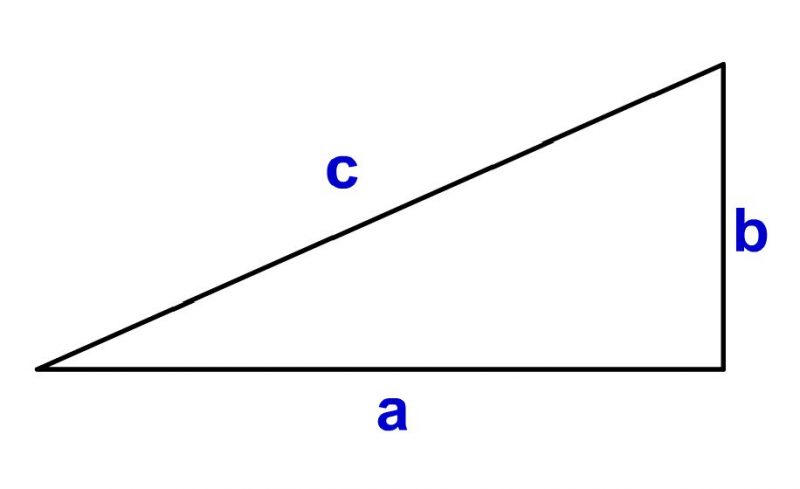
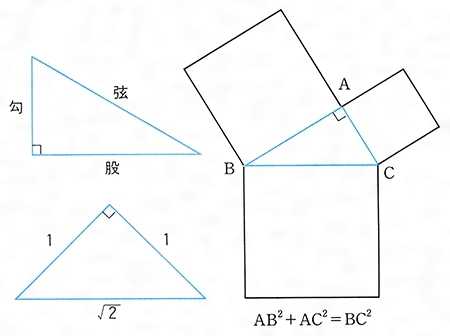
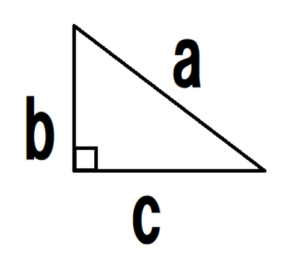
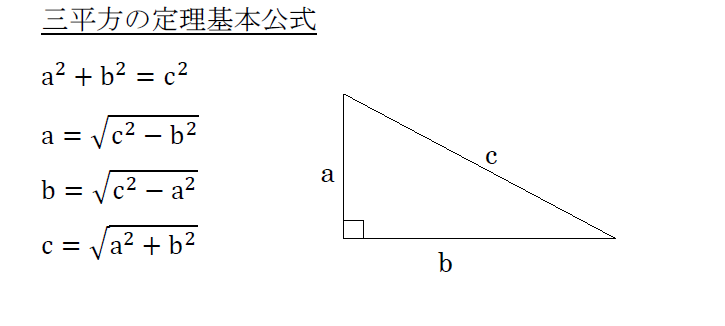
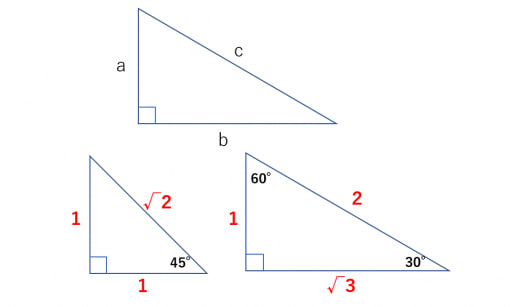
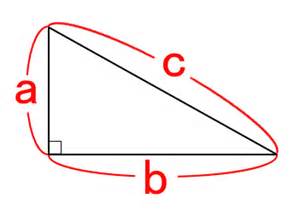
三平方の定理 公式 一覧-接弦定理、および、∠P は共通なので PTA ∽ PBT 従ってPT PB = PA PT ∴ PA×PB = PT2 324 三平方の定理 直角三角形の斜辺の2 乗は、その他2 辺の2 乗の和になる a2 b2 = c2 A B a C b c 325 ピタゴラス数 a2 b2 = c2 を満たす正の整数の組(a,b,c) のことを、 ピタゴラス数と呼ぶ ピタゴラスの定理 ∠ A = 9 0 ∘ \angle A=90^ {\circ} ∠A = 90∘ なる直角三角形 A B C ABC ABC について A B 2 A C 2 = B C 2 AB^2AC^2=BC^2 AB2 AC 2 = BC 2 誰もが知っている有名な定理だと思います。 →三平方の定理の4通りの美しい証明
三平方の定理 公式 一覧のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  | |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
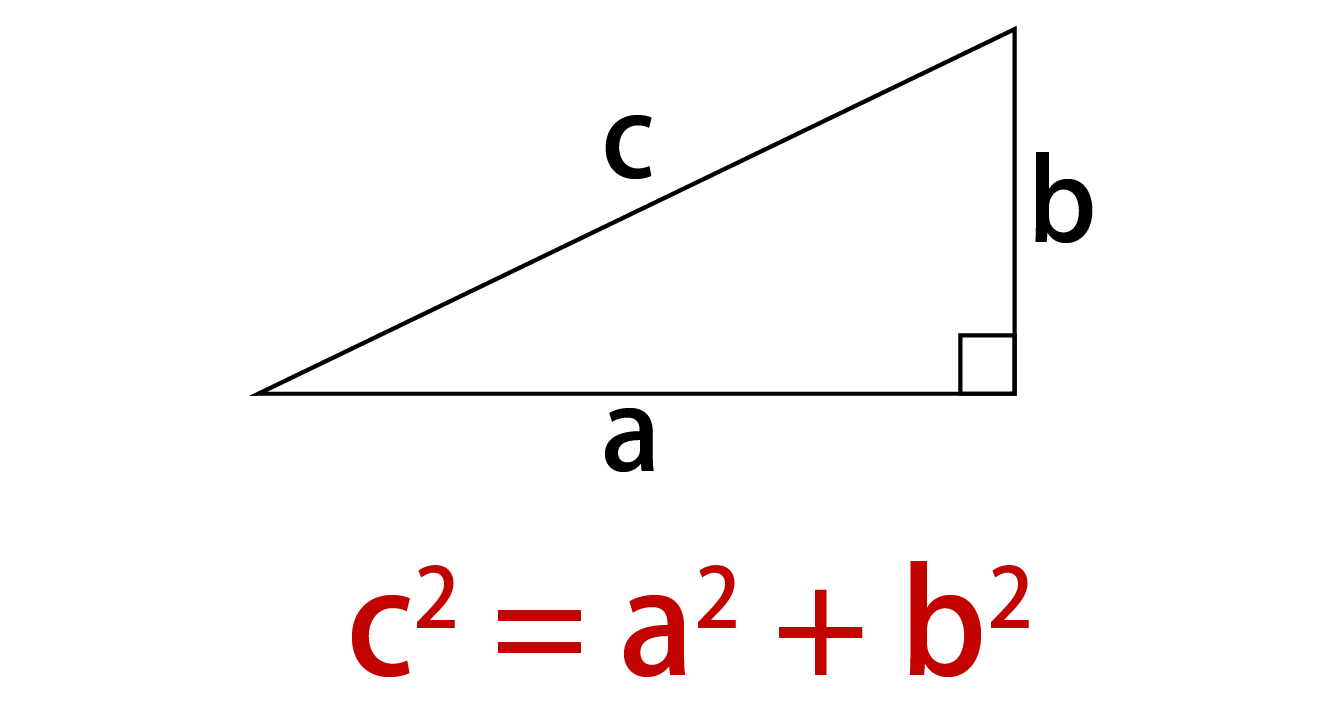 |  | |
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 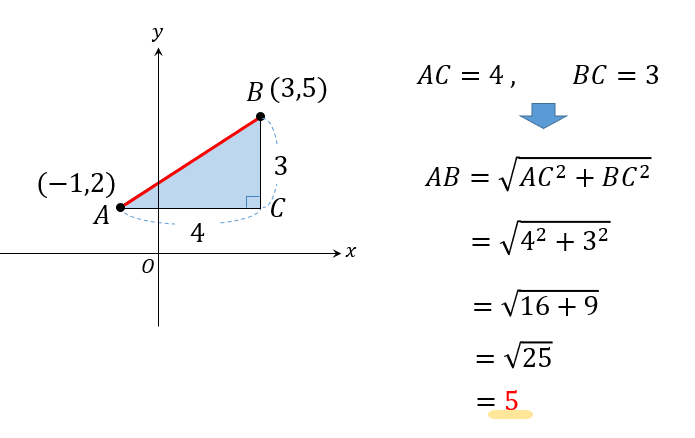 | |
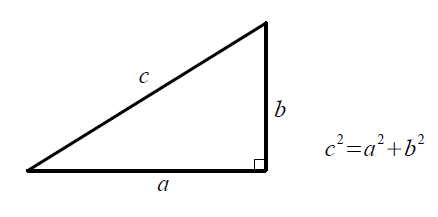 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 公式 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
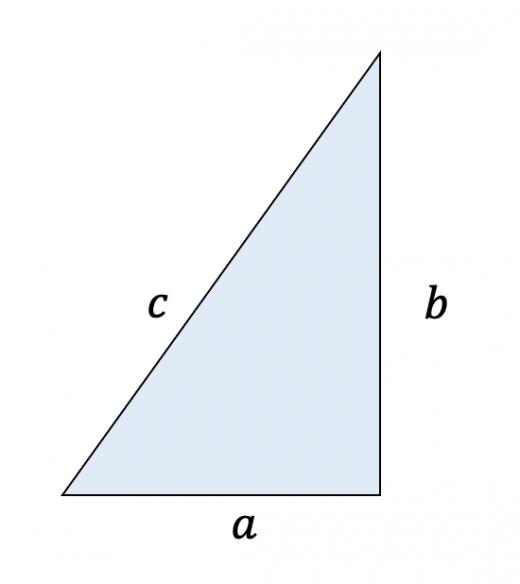 |
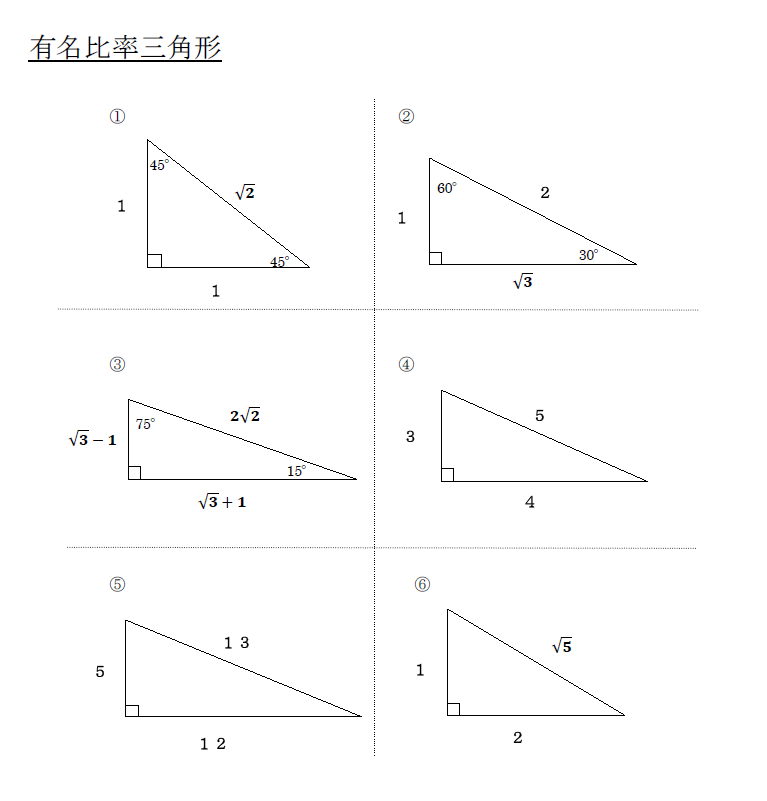
三平方の定理 別名 ピタゴラスの定理 世界中の 古文書に 記述が 見られるこの公式 現代の 実生活においてなお 極めて 有用な この定理。 直角三角形の直角を挟む両辺のながさの 2乗の 合計は 残りの1辺の2乗に 等しい。三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。
Incoming Term: 三平方の定理 公式 一覧,




0 件のコメント:
コメントを投稿