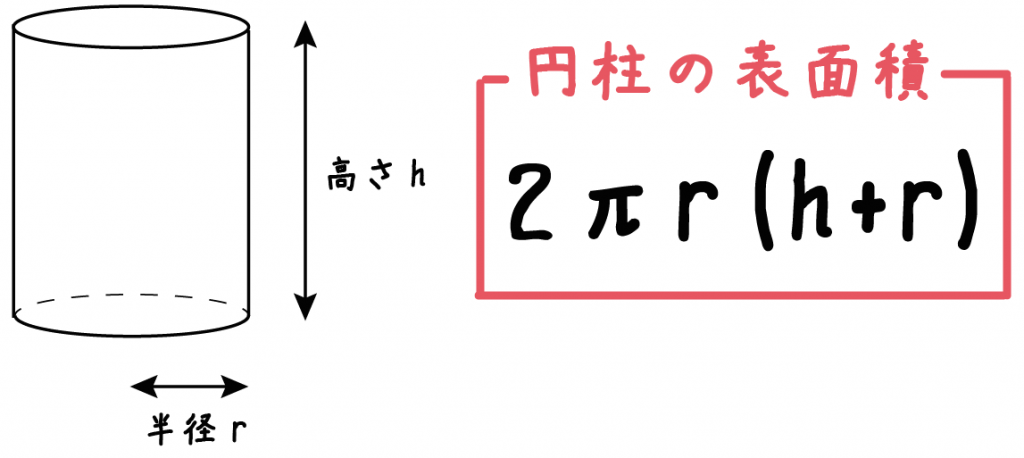
表面積 表面積を求めるには 立体の 各面の面積 を求めて、その和を出す。 できるだけ 展開図を描いて求める ようにする 柱 柱には底面が2つある。そして側面は長方形になる。 表面積はこれらの面積をそれぞれ出して和を求める。回転体の表面積の公式 (Ⅰ) 区間a,b で連続,区間(a,b) で微分可能な曲線 y =f (x) とx 軸 とで挟まれる図形を x 軸のまわり に回転してできる回転体の曲面の 表面積S は,次式で計算できる。 S =2π∫ a b y √ 1+(dy dx) 2 dx (Ⅱ) 区間c,d で連続,区間(c,d)① 立体のすべての面の面積の和を表面積という。また,側面全体の面積を側面積,1 つの底面の 面積を底面積という。 ②(柱体の体積)=(底面積)×(高さ),(柱体の表面積)=(側面積)+(底面積)×2 問題1 右の図の角柱の体積と表面積を求めよ。

1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
立体の表面積と体積
立体の表面積と体積- 球の表面積の求め方の公式を1発でおぼえる方法 をひそかに伝授しよう。公式をおぼえたいときに参考にしてみてね^^ 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえでは、表面積はいくらになったでしょうか。また面を1つずつ数えてみて下さい。 表面積は「24」になってますね。 すなわち、体積が8倍になっても、表面積は8倍の「64」にはならないことが分かります。 ×体積8 : 表面積48 ではなく、 体積8 : 表面積24 という比です。 この関係は、仮に体積を




スタディピア 立体の表面積
面積の公式はπ r 2 なので、 π r 2 =36π r =6(cm) 半径=6cmなので、 直径は、6×2=12(cm) ≪答≫ 12cm ※水面の半径を求めてからも解けるから試してみてね! <前: L37 相似な立体の表面積と体積の比 の問題 『第5章 図形と相似』の復習テスト の問題• 立体構造からのデ タ抽出立体構造からのデータ抽出 – 2次構造 – 溶媒露出表面積溶媒露出表面積 • 立体構造比較 – 立体構造重ね合わせ立体構造重ね合わせ – 立体構造分類データベース • 立体構造データの統計解析 – 非冗長立体構造データベース立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例 円錐の立体角は、 $2\pi\left(1\cos\theta_0\right)$ という公式で計算すること
底面の円の半径を $r$ とすると底面積は $\pi\, r^2$ になるので、円錐の体積の公式は次のようにも表わせます。 体積 $V=\dfrac{1}{3}\pi\, r^2\, h$ 球の体積を求める公式 体積 $V=\dfrac{4}{3}\pi\, r^3$ ちなみに、球の表面積を求める公式は、 表面積 $S=4\,\pi\, r^2$ です。 円錐の表面積の求め方がわかる3ステップ 円錐の表面積は3ステップで計算できちゃう^_^ つぎの例題をときながらみてみよう。 半径3cm、母線の長さが10cmの円錐の表面積を10秒以内に計算して。 Step1 底面の「円周の長さ」を計算したる まずは底面の「円周漢字のとおり、立体の 「表面の面積」 のことだよ。 底面や側面など、 すべての面の面積 を求めて、たし合わせよう。 立体の表面積を求めるときのポイントは、これだよ。
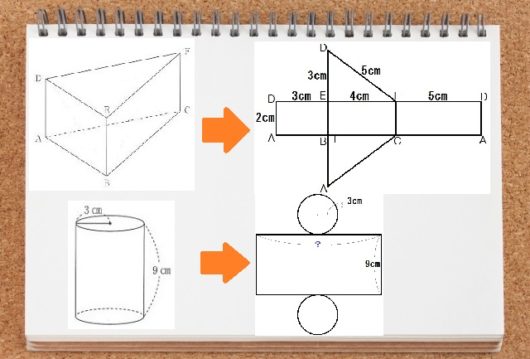
表面積や体積の求め方 (三角柱,四角柱,円柱,球や半球) 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。数学16章空間図形「立体の表面積と体積」<準備問題①> 組 番 名前 面積や体積の表し方や求め方について,次の問いに答えなさい。 (1)次のア~ウの面積を求めなさい。 (1マス1㎝の方眼で,イの縦の長さは05㎝とする。) ア イ ウ 1㎝2 立体の表面積を聞かれたら、展開図を書こう! ということ。展開図さえ書けば、そこに見えるのは長方形であったり、円であったり。ただの平面図形です。 それらの面積を1つ1つ出してから足し合わせるだけ。シンプルです。 立体の体積 表面積の後は



1



立体の体積と表面積 1 柱体の表面積
Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。立体の表面積(東京女子学園中学 10年) 立体を重ねた表面積(立教新座中学 10年) 立方体のくり抜き(慶應義塾普通部 10年) 表面積比から求める体積(東海中学 12年) どんな立体でしょうか?(カリタス女子中学 12年) 複雑な立体のようですが・・・(立教池袋中学 11年) 穴のあい立体は円柱になり,表面積は底面積×2=16 π ×2 (cm 2)と側面積8 π ×7 (cm 2)の合計になります 底面積2つで32 π (cm 2),側面積56 π (cm 2)の合計は π (cm 2)



1




Sqrt3 6cm 0 Descubre Como Resolverlo En Qanda
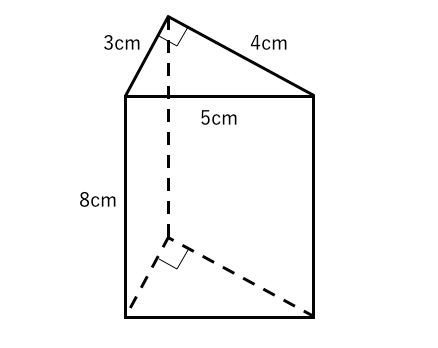
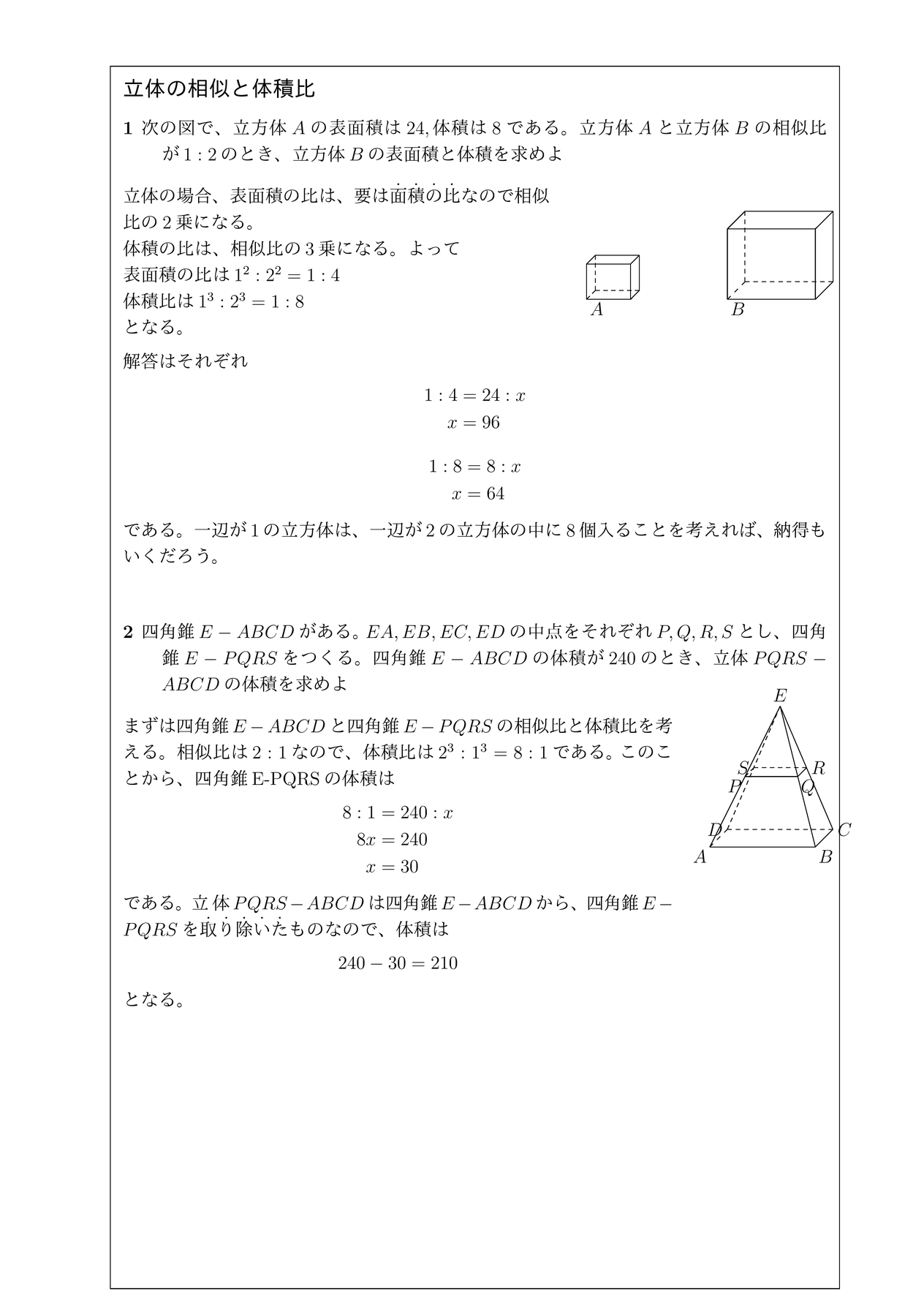
算数 小学生 中学受験 算数 複雑な立体の面積と表面積 前半直方体や立方体をもとにした複雑な立体の体積や表面積の求め方を学習します別の解き方として、「相似な立体の表面積比は相似比の2乗比」であることを使うと、次のように簡単に求まります。 \begin{align*} S_1 S_2 &= 1^2 2^2 \\ &= 1 4 \end{align*}23 三角錐の表面積 右の図は,1辺の長さが 3 cm の立方体 ABCD EFGH である。 この立方体を3点 B, D, E を通る平面で2つの立体に分けるとき,2つの立体の表面積の差は何cm 2 か。



立体の表面積




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分についてまとめています。こ立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 四面体の体積 四面体の体積 四面体の6つの辺の長さから体積と表面積を計算します。 正四面体の体積 正四面体の体積図1の直方体4個分の表面積の和と図2の立体の表面積の比は 5:4となりました。 図1 図2 (1)「あ」の長さは何cmですか。 (2)図2の立体を2個作ってぴったり重ね、 上の立体を点Pを中心に45°回転させて、図3のような立 体を作ります。



立体の表面積を求める 練習問題 苦手な数学を簡単に




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
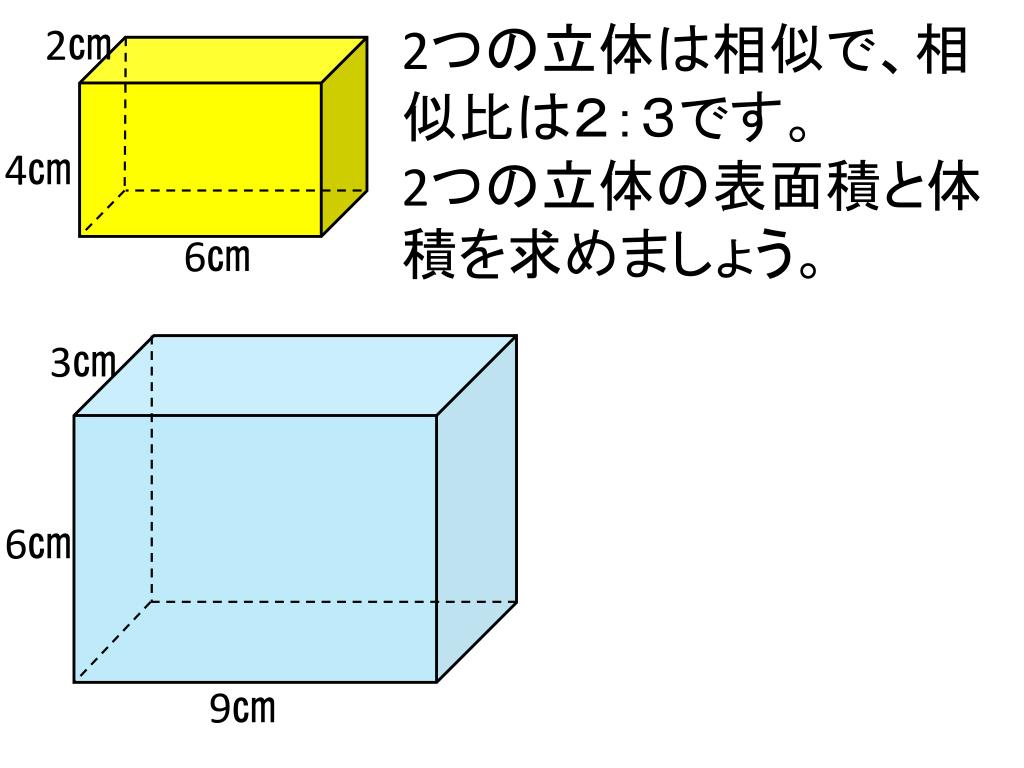
相似比と表面積と体積の関係 相似な図形が2つあり、相似比がa:bならば、表面積比は a²:b² 、体積比は a³:b³ になります。 注意:相似な図形である場合に限ります。 では問題です。 図のように三角錐O-ABCの底面ABCに平行な平面Lが、辺OAと点Dで表面積問題より→ちょっとややこしい立体の表面積 見取り図より→塗られた面の面積は(東京成徳大学中学 10年) 体積問題より→表面積比から求める体積(東海中学 立体の表面積とは、表側にある面の面積をすべて足したものをいいます。 イメージとしては、空気にふれてる面ぜんぶってこと。 だから、基本となる求め方は 展開図をかいて求める というものです。 以下、例題とともに見ていきましょう。 角柱の表面積 19 神奈川県公立高校入試問題 6




スタディピア 立体の表面積



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
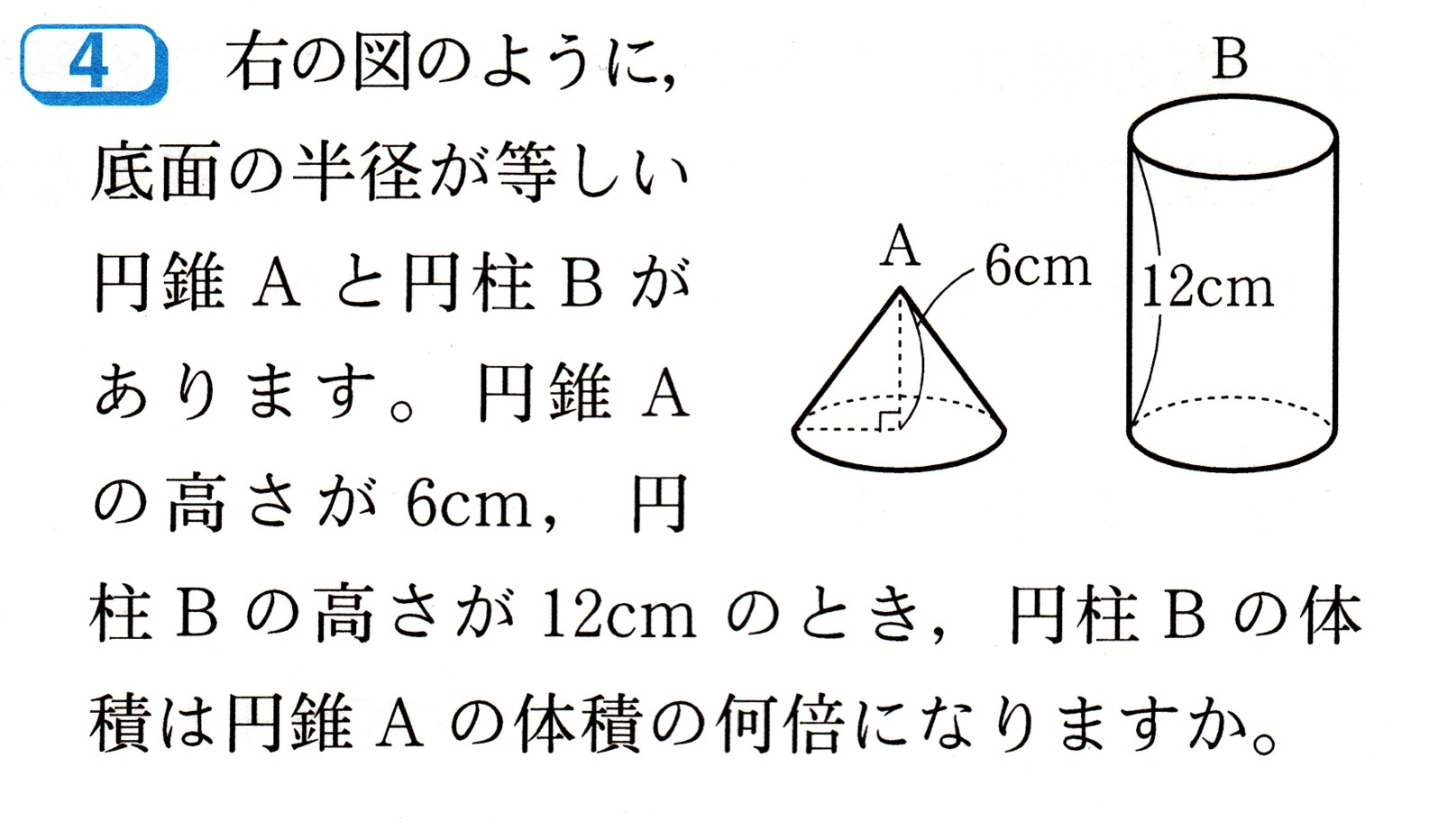
立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm 面の横の長さは底面の円周と同じに長さになるよ! 底面積 2×2×314=1256 1256×2=2512㎠ 側面積 10×4×314=1256㎠ (側面は1つしかないから2倍しないよ) 全部足すと、=㎠ どうかな? (2)側面積で迷った子も多いとおもうけど、 「展開図の横の長さ=底面の円周」 がわかったら大丈夫だよ! ぼたん (2)がとくに難しかったよー。 何回かやってV = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は




スタディピア 立体の表面積



Http Www Study X Com Syotesttyu1 Rittainohyoumenseki Pdf




誰でもわかる数学 中学1年 立体の表面積 円錐 Youtube




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円錐とは 体積 表面積の公式や求め方 受験辞典




表面積の求め方 計算公式一覧



中学数学 空間図形 表面積の問題のコツ



Http Www Edu C Pref Miyagi Jp Tangen Math Jun1 Math Comment 23hop Pdf



中学1年数学 立体の表面積と体積 確認問題4 あんのん塾



12年前期 千葉県公立高校入試 数学 第2問 3 立体図形の体積 表面積 配点5点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト




複雑な体積 表面積の問題 家庭教師としの勉強部屋




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




中学生 立体の体積と表面積のノート一覧 Clear




立体の表面積 小学生算数です教えて下さい Okwave



無料 中1数学 基本問題 解答プリント 空間図形5 立体の表面積 142



中1 空間図形 4 立体の表面積 2 学習支援 まなびの函




立体の表面積 無料で使える中学学習プリント




角柱 円柱の表面積と体積の公式 数学fun




表面積




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1 数学 中1 立体の表面積 Youtube




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




角錐 円錐の体積と表面積の公式 数学fun



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典




切断面のある立体の表面積 算数の問題 身勝手な主張




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun



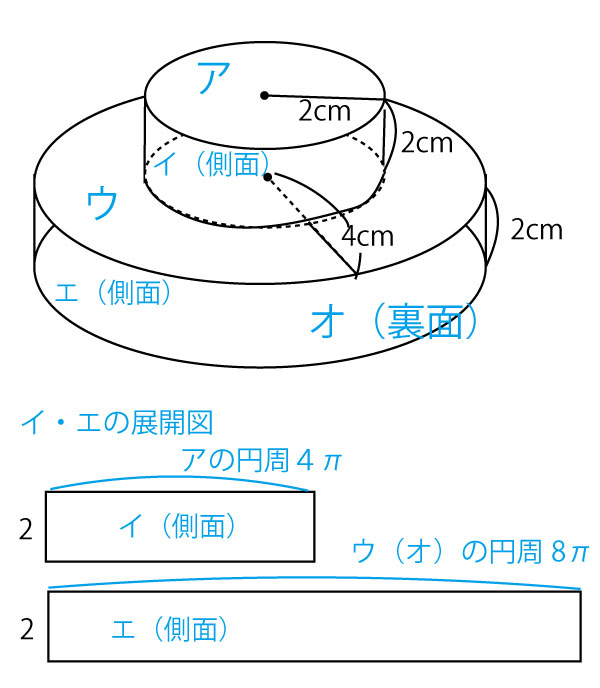
立体の相似と表面積比 体積比 チーム エン



1




表面積の求め方 計算公式一覧
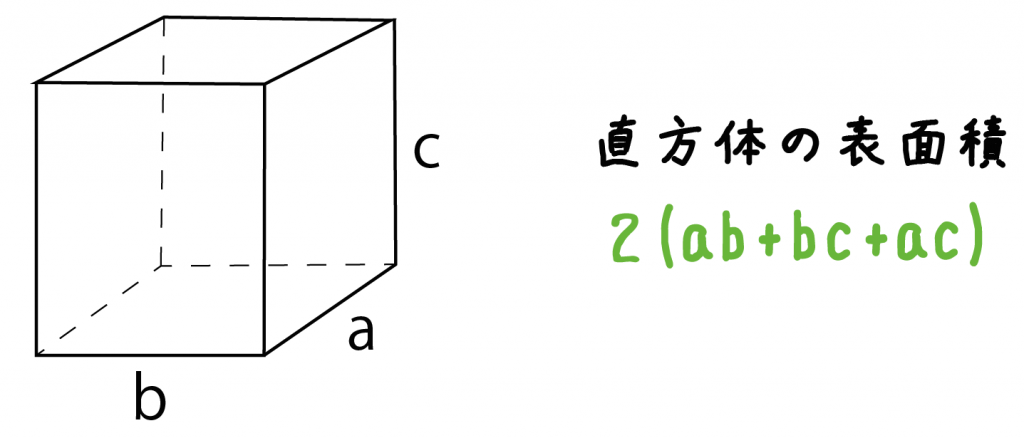



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
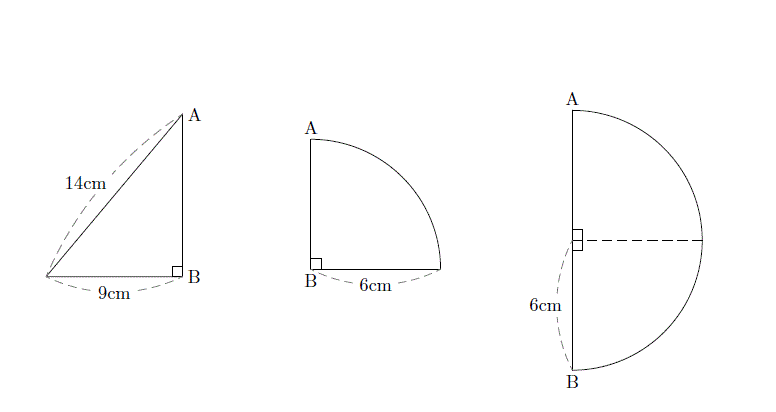



かみのドリル 立体の体積と表面積 回転



1




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の表面積 Hobofoto



立体 の 表面積 求め 方



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー




シュウモン No 27 くりぬいた立体の表面積 小学5年生 最高難易度 若松塾大久保校ブログ



Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id




3d100 Descubre Como Resolverlo En Qanda



中学1年の数学 動画 立体の表面積の問題 19ch



中学1年数学 立体の表面積と体積 確認問題6 あんのん塾




立体の表面積 無料で使える中学学習プリント




スタディピア 立体の表面積




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット
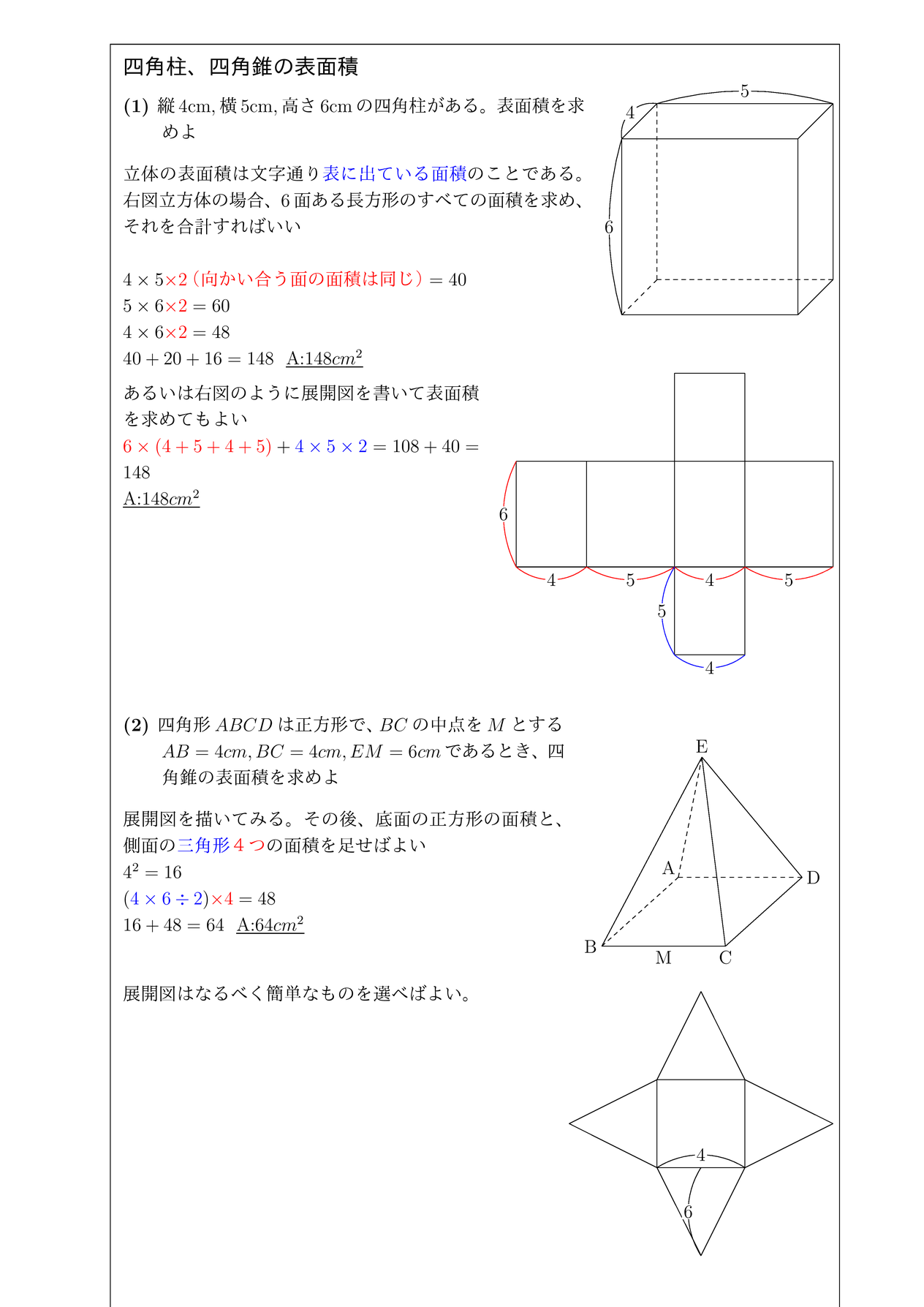



四角柱 四角錐の表面積 チーム エン



立体図形の表面積 桜蔭中学 17年 解けるかな 算数の難問に挑戦




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中1数学31 立体の表面積と体積 Youtube
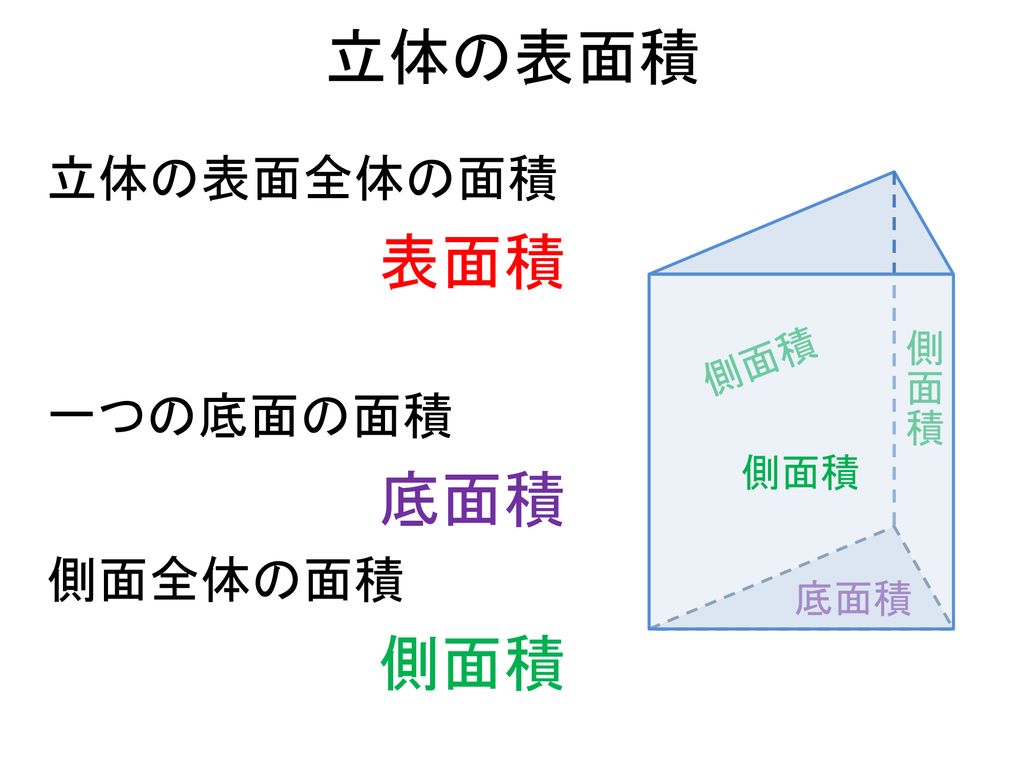



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download



立体の表面積と体積 わかる数学



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




5章3節2 相似な立体の表面積や体積の比 数学のすすめ




円柱の表面積と体積を求める公式 具体例で学ぶ数学



Studydoctor柱体や角錐の表面積の求め方 中学1年数学 Studydoctor



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 このページの問題プリント 全部
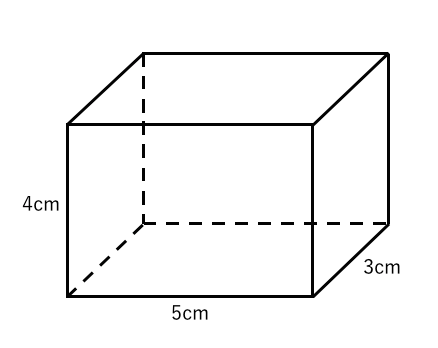



立体の表面積を求める 基本問題 苦手な数学を簡単に
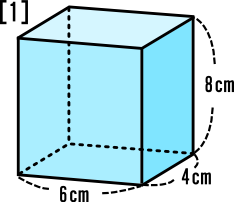



中学1年数学練習問題 立体 円錘 三角錘等 の表面積の求め方と解答



立体の表面積



この問図形の表面積と体積を教えてください 上の円錐と円柱 Yahoo 知恵袋




中1数学 立体の表面積 例題編 映像授業のtry It トライイット



Http 219 122 57 117 Attach 6629 Jmw 1b6 4 Pdf




中1数学 立体の表面積 練習編 映像授業のtry It トライイット




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



図形の計算が分かんないので教えてくれると助かります 半球と Yahoo 知恵袋
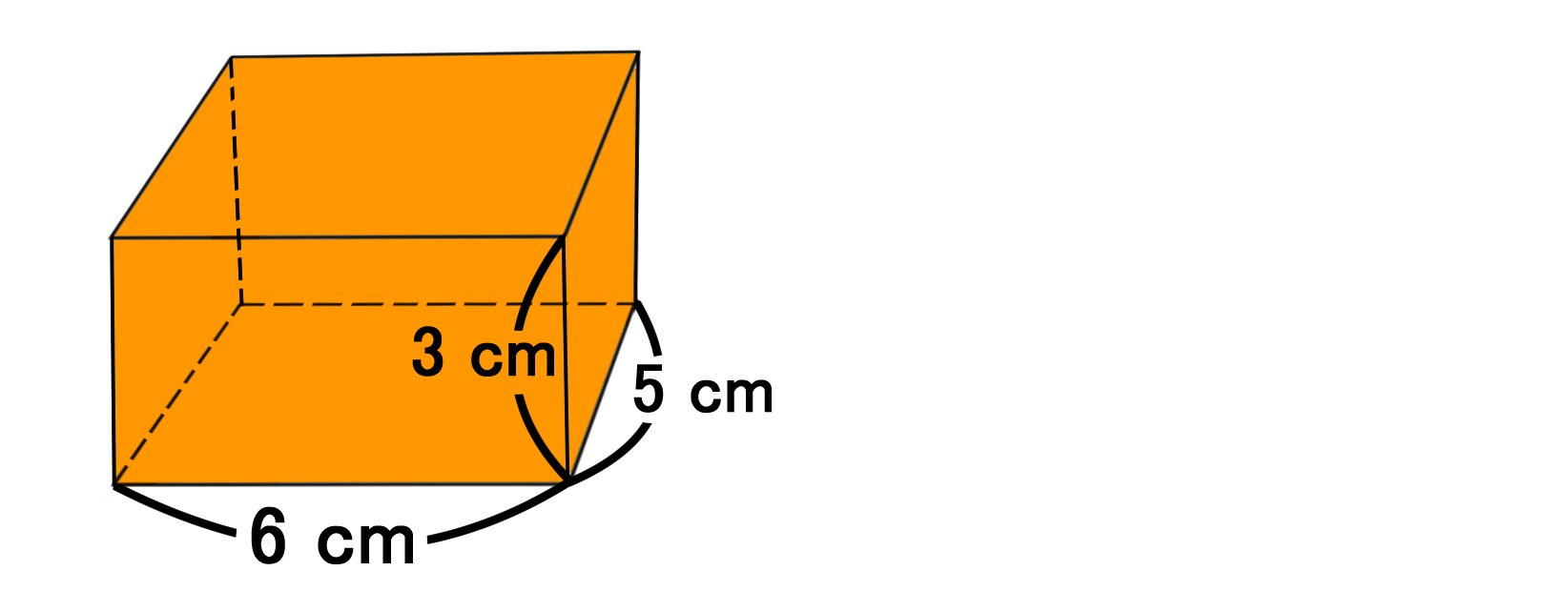



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



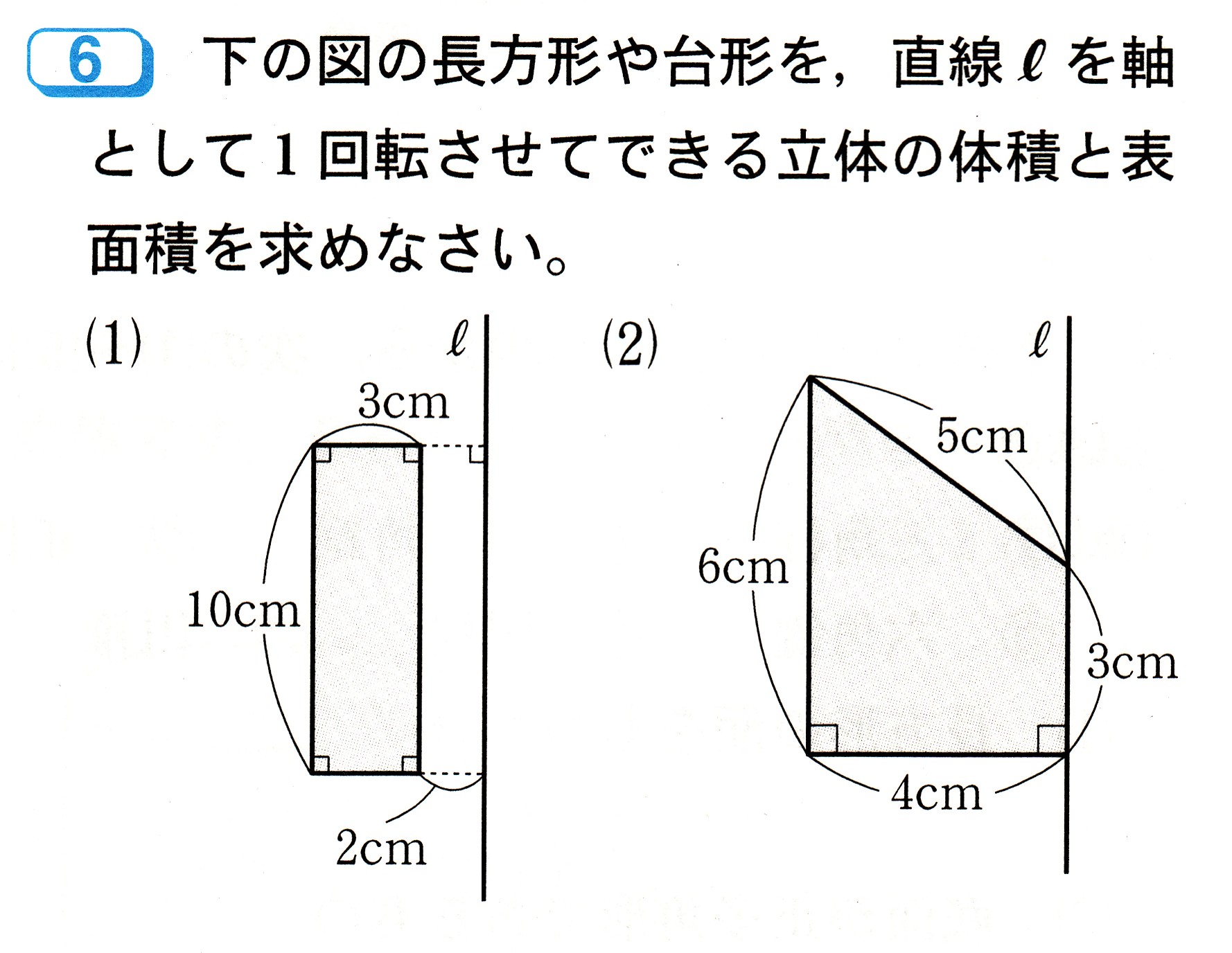
6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2



球の表面積 立体の表面積が影の面積の4倍になること 数学と社会の架け橋 数学月間




4角柱の立体の表面積の求め方が分かりません 答えは432cm になるそうです Clear
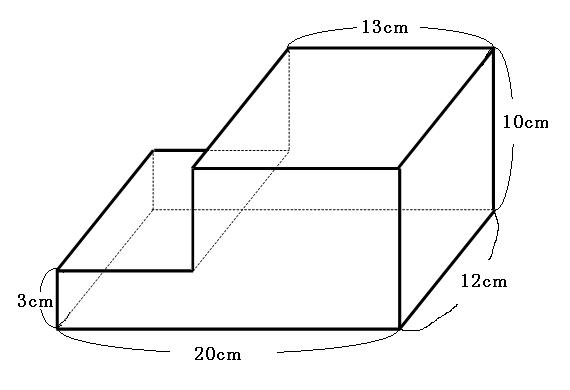



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
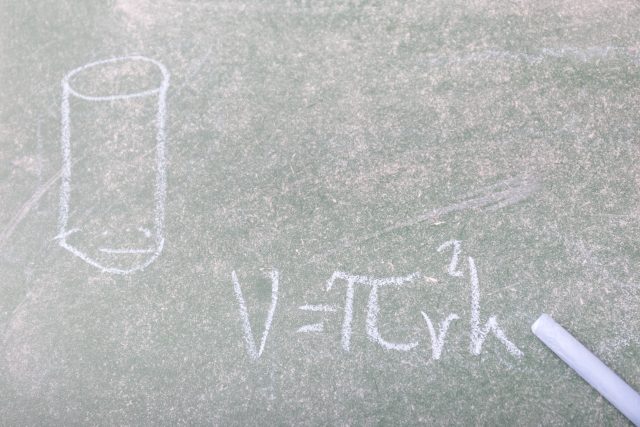



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



かまぼこ型の表面積 立体図形 パズル おもしろ算数問題



無料 中1数学 発展問題 解答プリント 空間図形5 立体の表面積
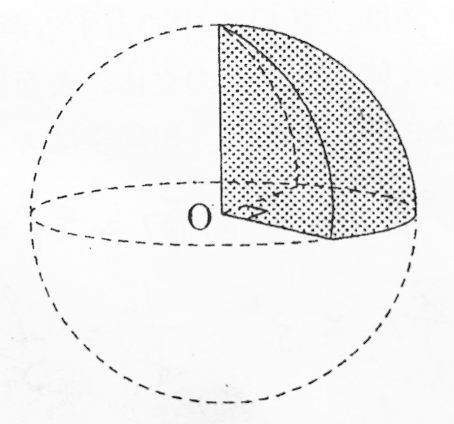



球の問題 苦手な数学を簡単に




中学入試 立体の表面積は につながる 積み木の思考力問題 小学校受験 親子で取り組む小学校受験 Tsubasa通信教育



6 13 第6章 空間図形立体の表面積と体積 角柱や円柱の体積 ニュージーランド短期留学ダイアリー




表面積の求め方 計算公式一覧




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




スタディピア 立体の表面積
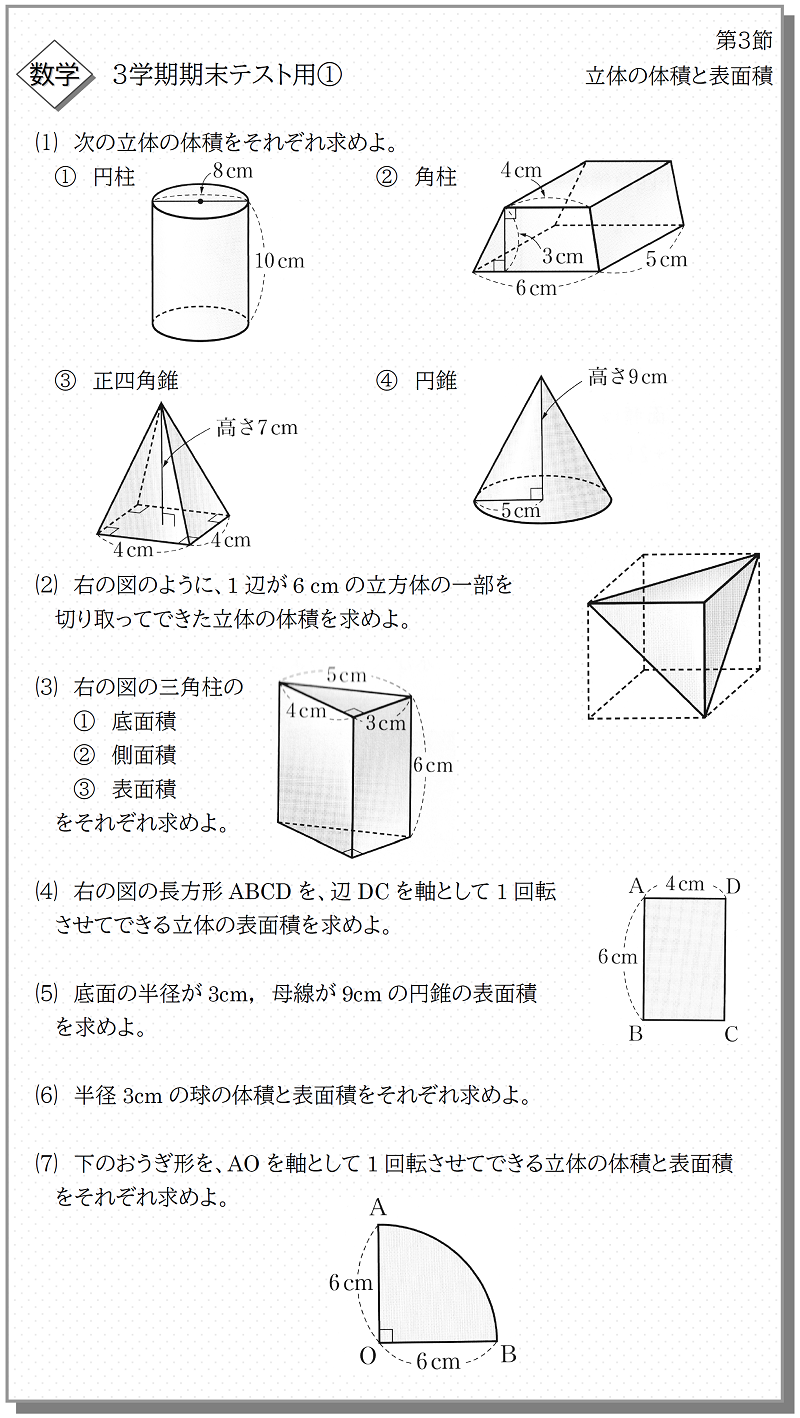



中1数学 立体の体積と表面積 教科書p194 5 3学期期末テスト 赤城 ᐡᐤᐡ



高校入試 英語 数学 学習 立体の表面積と体積




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




Nitter




Lihat Cara Penyelesaian Di Qanda
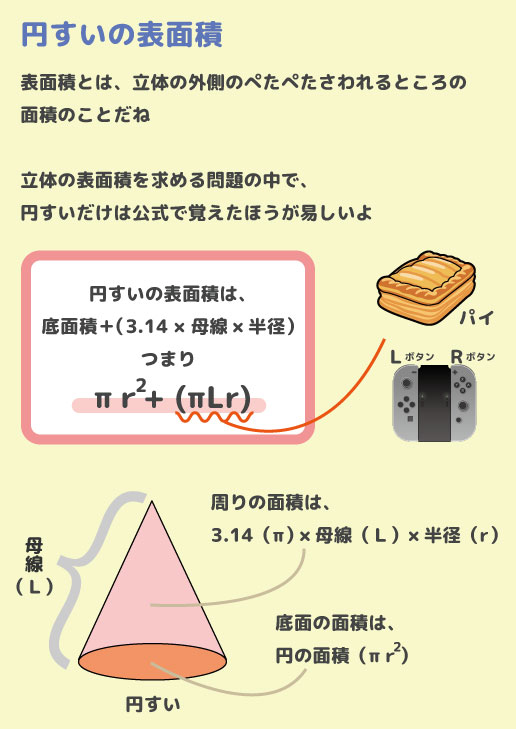



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




円柱の表面積 Youtube



0 件のコメント:
コメントを投稿