中2数学 150 簡単公式2直線の交点の座標を3秒で計算できる求め方 中3数学 因数分解で二次方程式の解を求める5ステップ 求積公式の発見 直方体の体積=縦×横×高さ 立方体の体積=1 辺×1 辺×1 辺 学習者 基点の学び 5 2いろいろな体積の単位 立方体の体積の求め方に公式ってあるの?? こんにちは!この記事をかいているKenだよ。茶漬けを食べたいね。 立方体の体積の求め方には公式があるんだ。 立方体の1辺の長さをaとすると、その体積は、 aの三乗 で求めることができるよ。 つまり、立方体よって立方体の体積=2×2×2=8です。 また、上記の公式をみると「立方体の体積が分かっていれば1辺の長さが逆算できる」と分かります。 例えば立方体の体積=m 3 のとき1辺の長さは約27mです。

公式を図解 すい体の体積 円すいの表面積の求め方
立方体の体積の求め方 公式
立方体の体積の求め方 公式-立方体と直方体って何が違う? 立方体の体積問題を解説! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがで 立方体の体積の計算問題を解いてみよう それでは、立方体の体積の求め方に慣れるためにも計算問題を解いていきましょう。 ・例題3 1辺の長さが2cmの立方体の体積はいくらでしょうか。 ・解答3 上の立方体の体積の公式を元に計算していきます。
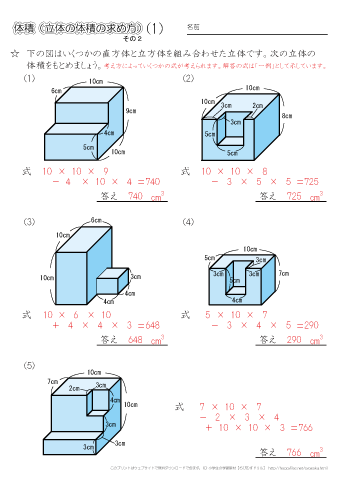



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
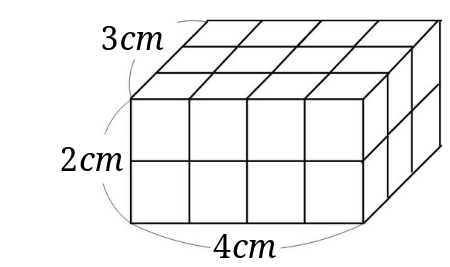
立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun 体積の求め方 計算公式一覧 計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすくそれぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)立方体 直方体 断面積から体積計算 公式 求め方 高さ 底面積 自動 volume
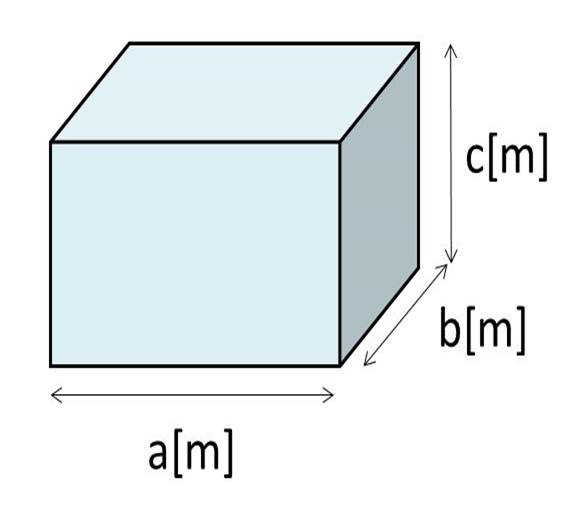
立方体や直方体、そして円柱のような立体の体積はすべて、(底面の面積)×(底面を面と垂直方向に平行移動させた距離)を計算することで求まります。 したがって、上図のような斜円柱の体積の求め方も直円柱同様に、 $ V=Sh $ で求めることが出来ます。5年 直方体と立方体の体積|算数イメージ動画集|大日本図書 文部科学省『教育用コンテンツ開発事業』 直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ=直方体の体積,1辺×1辺×1辺・「体積」の用語を復習する。 1cm 1c㎥ 1cm 1c㎥ 算数科学習指導細案 5年 「体積」 本時の目標 直方体の体積の求め方を考えることができる。 辺の長さを用いることで、直方体や立方体の体積は計算によって求めることが できることを知る。
簡単公式台形の体積(正四角錐台)の求め方がわかる3ステップ 中2数学 折り返した図形の角度を求める2つのコツ 中1数学 中学数学球の表面積の求め方の公式を1発で覚える方法 中1数学 153 図を見てみると、一辺が\ (1cm\)の立方体が、たてに3つ、横に4つ、2段になっています。 この立方体の数を求めると、$$3\times 4\times 2=24$$一辺が\ (1cm\)の立方体が24個あることが分かりました。 この直方体の体積は、\ (24cm^3\)と言うことが分かりました。直方体や立方体の体積 ・体積の意味と測定 ・体積の単位(㎤,㎥) ・直方体,立方体の体積の求 め方と公式 ・容積の意味 第6学年 角柱と円柱の体積 ・底面積の意味 ・角柱,円柱の体積の求め方 と公式 面積レ ル3 複合図形 体積レベル3 複合図形




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




6年算数立体の体積1 教え方
(イ)立方体及び直方体の体積の計算による求め方について知ること。 イ 次のような思考力,判断力,表現力等を身に付けること。 (ア)体積の単位や図形を構成する要素に着目し,図形の体積の求め方を考えるとともに,体楕円体の体積 腎臓の大まかな体積の確認目的。 楕円体形状の腎臓動脈瘤の塞栓で、使用するコイルの適合サイズを表面積で推測するのに使用しました。 大変役に立ちました。 ありがとうございました。 学校の宿題に使いました。 ありがとうござい 錐の体積の公式の求め方 ① 立方体を用意する。 そのまんまです。1辺がaの立方体を書いてみましょう。 1辺がaなので、この立方体の体積は、 a×a×a=a 3 ですね。 下の図をイメージしてください。 ② 中心に点を打つ。



Excel エクセルで立方体 直方体の体積の計算を行う方法 立方メートル 白丸くん



6年算数立体の体積1 教え方
今日も、直方体,立方体の体積について学習をしていきます。 めあてを読んで、ワークシートに書きましょう。 めあて 直方体と立方体の体積を、計算で求める方法を考えよう。 (3)㋒の直方体の体積の求め方について考えていきます。 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、体積の公式を想起する。 縦×横×高さです。 一辺×一辺×一辺です。 体積の公式の意味を確認する。 1c㎥の立方体がいくつ並ぶかを数えるた めです。縦に幾つ並んで、横に何列で、何 段積み重なっているかで、全部の個数が分 かります。



直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方
立方体の体積 《円・半円・弧・扇形》の円周・面積の求め方と公式一覧|小学生の算数 円に関係する公式4種類をまとめました。 重要な公式なので確実に覚えるようにしましょう。️ 立方センチメートル 体積の単位 は数を 3回かけて計算します。 今回は立方体の体積の計算、単位、公式、求め方、リットルとの関係について説明します。 第一のまとめ かいだん形の体積は直方体に直すと求めることができる。 7指導案例 画面例 体積の求め方 1:このソフトの機能とねらい 直方体の体積が「1㎝3のいくつ分」で数値化できることを提示するシミュレーション ・直方体の体積は1㎝3の立方体を敷きつめていくことにより数値化できることが視覚的に理 解できる。




どうして1 3なの 錐の体積の公式の求め方 まなべーと



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
5年算数 体積の教え方1 子どもの学習支援by いっちに算数 体積の勉強は、体積の単位 や を理解させるとわかりやすくなります。 そのために2年「かさ」や4年「直方体と立方体」の勉強を元にして考えさせたいと思います。 忘れているお子さんには、上のリンク先でおさらいさせましょう。立方体の体積 110 /16件 表示件数 5 10 30 50 100 0 1 1532 男 / 歳未満 / 小・中学生 / 少し役に立った / 使用目的 2x2ルービックキューブの体積を求めるため 2 2127 男 / 歳代 / エンジニア / 非常に役に立った / 使用目的四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 10 女 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かり



5年算数体積2わかる教え方




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
直方体と立方体を組み合わせた立体の体積を求める問題を繰り返し練習できます。 当ページのプリントの解答では、解答式を一例としてのせています。 どのように式を組み立てて立体の体積を求めるかは様々な考え方があります。 学校のテスト等では 求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8× 8×4 =256(cm³) ②の立方体の体積=4×4×4=64(cm³) よって求める立体の体積=256+64=3(cm³)教え方4-① 大きな直方体や立方体の体積を計算して求める方法に気づかせ、 (立方メートル)の単位を教えます。 問題 下図の直方体の体積を求めましょう 直方体の体積は、たて×横×高さで求められるので、cmで表すと 300cm×400cm×0cm = となります。



5年算数体積2わかる教え方




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス
立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle教え方1 教え方1 5年生で勉強した直方体や立方体の体積の求める公式を生かして、四角柱の体積の求め方を気づかせます。 5年で勉強した 立方体と直方体の体積 の求め方をふりかえります。 立方体の体積=1辺×1辺×1辺 直方体の体積=たて×横×高さ 5年 体積が求められるようになると1番最初に扱う立体が、立方体や直方体です。 立方体の体積を求める公式は、「一辺×一辺×一辺」。 直方体の体積を求める公式は、「たて×横×高さ」です。 覚えてしまえば、簡単に体積が求められますが




Descubre Como Resolverlo En Qanda
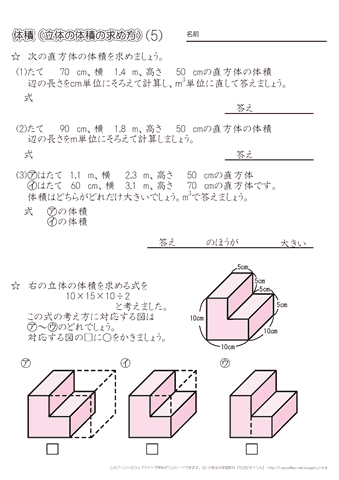



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
直方体・立方体の体積の求め方と公式 中学1年 〇基本的な柱体,錐体の体積の求め 方 球の体積の求め方 厚さ1㎝の板で作った,左の図のような直方体の形をした入れ物があ ります。にしくんはこの容積の求め方を次のように考えたところ,体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



1
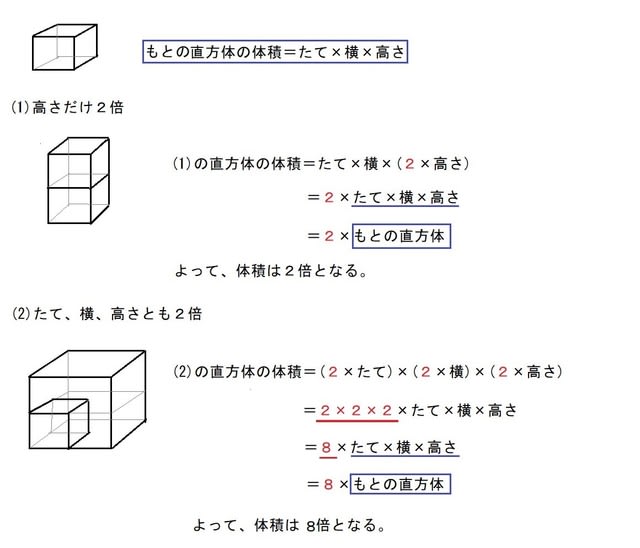



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support



1



5 5 複雑な立体の表面積と面積を求めるには さんすうがく
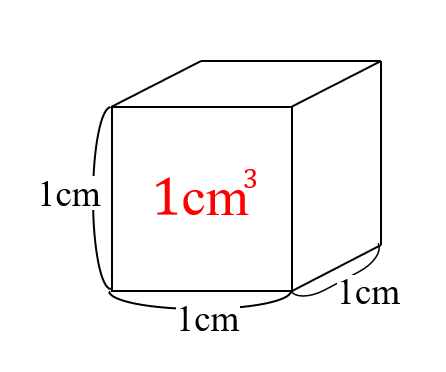



立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



地図の体積計測




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




球の体積と表面積 公式と計算問題と証明 Irohabook




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



5年算数体積2わかる教え方




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




小5 算数 小5 3 直方体と立方体の体積 Youtube




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
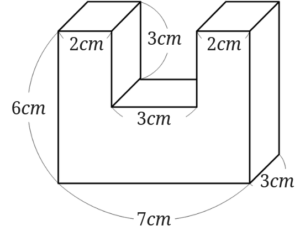



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
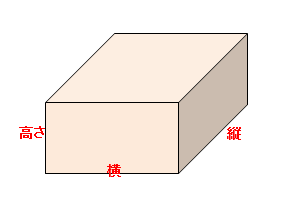



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




円柱の体積の求め方 公式 小学生 中学生の勉強




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




体積の求め方 計算公式一覧



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋




体積の求め方 計算公式一覧




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




体積の求め方 立方体 長方体 小学生 算数のノート Clear




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



円柱の表面積の求め方 立方体 円錐の投影図 中学1年数学 空間図形




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




三角錐 四面体 の体積の公式 Schoolmath S Diary




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ




公式を図解 すい体の体積 円すいの表面積の求め方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




小5 複雑な立体の体積 直方体 日本語版 Youtube




公式を図解 すい体の体積 円すいの表面積の求め方




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook
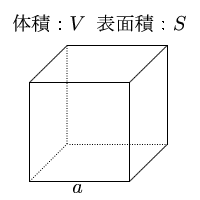



立方体の体積から1辺 体積 表面積の計算 計算サイト




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー



1




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
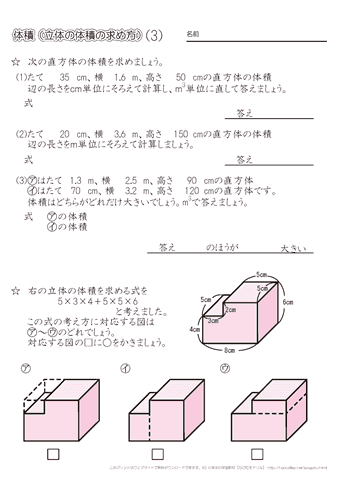



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




円柱の表面積と体積を求める公式 具体例で学ぶ数学




立派な 台形 体積 求め 方




直方体 立方体の体積 Youtube
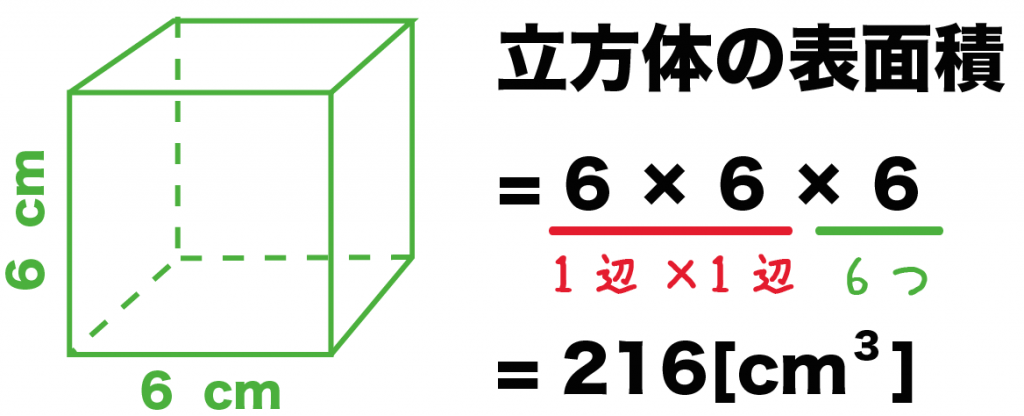



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




体積の求め方 計算公式一覧




体積 表面積




小5 算数 小5 5 体積の求め方のくふう Youtube




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf
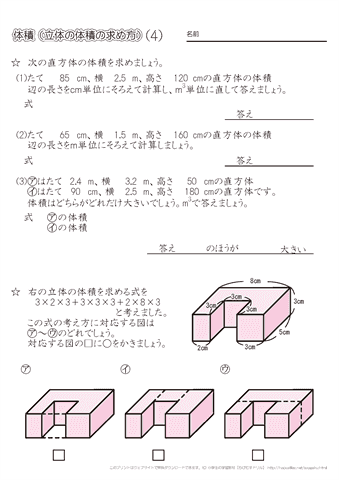



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




四角錐台の体積 高精度計算サイト




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



兵庫県実践事例 算数小学校6年



体積の応用
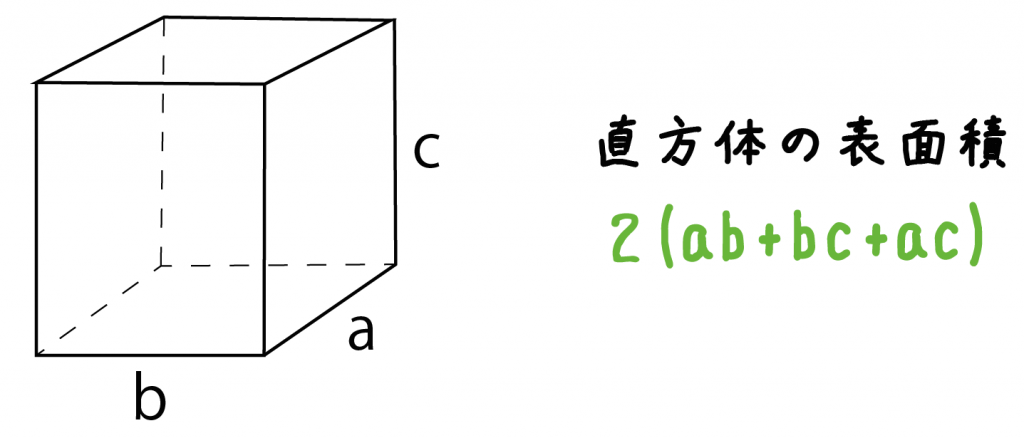



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
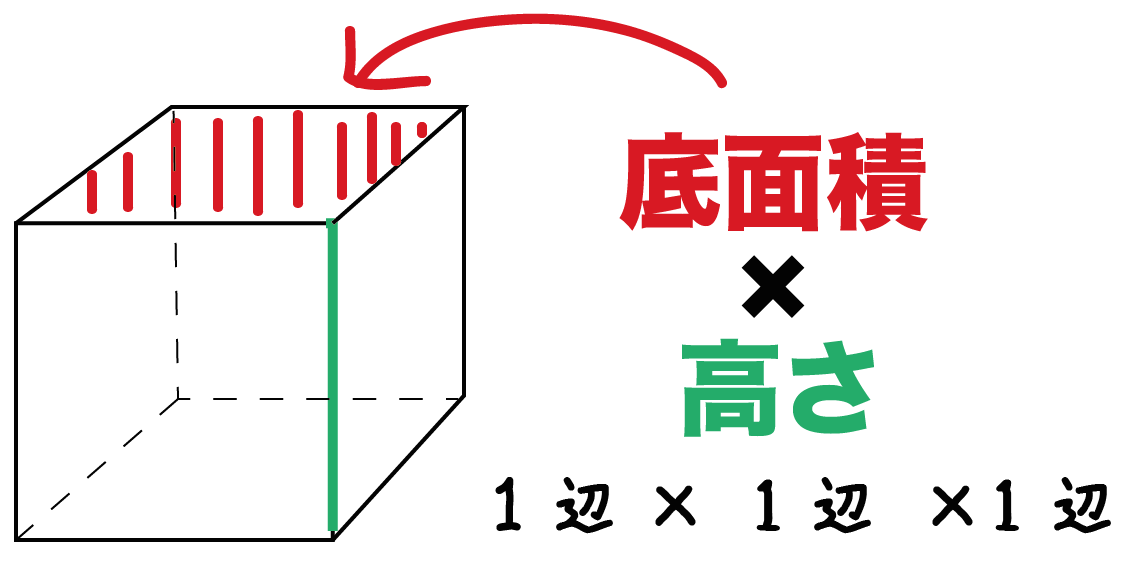



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧




立体の体積を求める公式
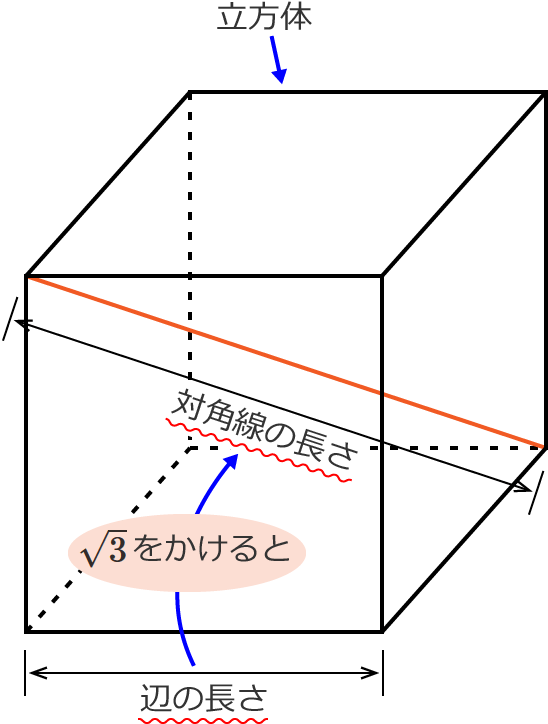



立方体の対角線の長さの求め方




円柱の表面積と体積を求める公式 具体例で学ぶ数学




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
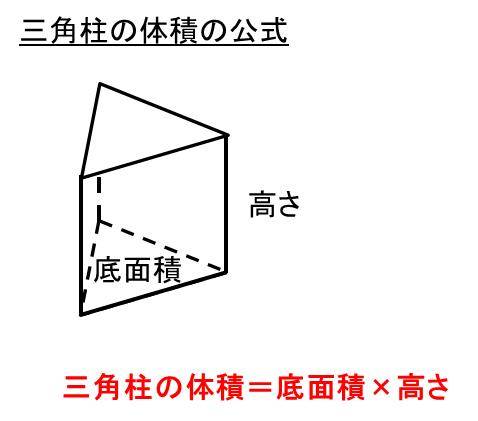



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム



1
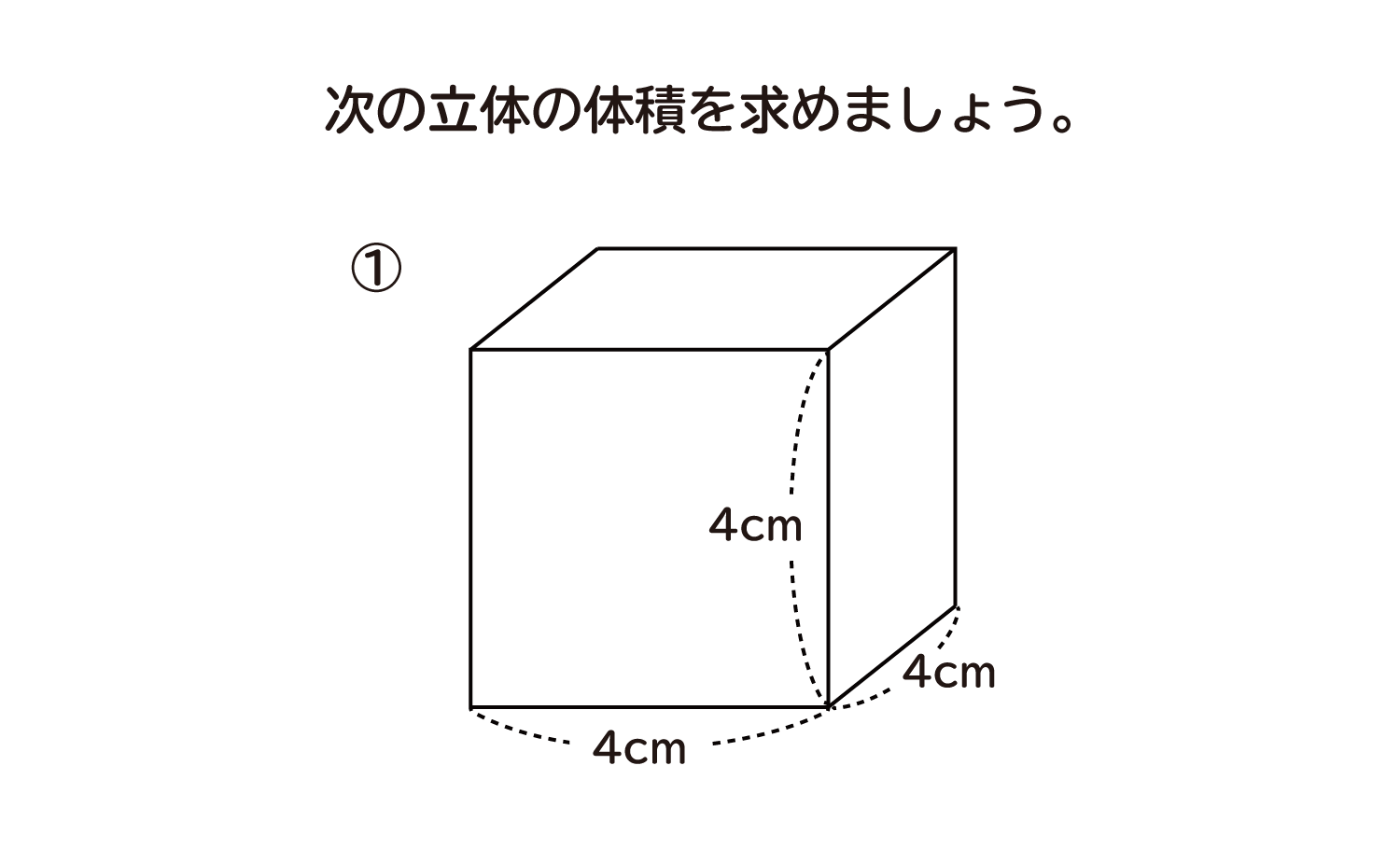



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



Math 積み重ねた立方体の表面積 働きアリ




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




どうして1 3なの 錐の体積の公式の求め方 まなべーと




円柱の体積の求め方 公式 小学生 中学生の勉強
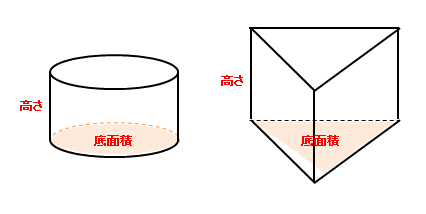



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー



0 件のコメント:
コメントを投稿